I just tried to proceed a bit, like this $ n!In the end we subtract $\sum^{1}_{n=0}\frac{(4n^28n3)2^n}{n!}$ since above we assumed $\sum^{\infty}_{n=0}$ calculus sequencesandseries summation taylorexpansion Share Cite Improve this question Follow edited Apr '16 at 351 fff asked Apr '16 at 329Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep

Coloring Coding Rational Expressions Really Helps Students Understand How To Simplify Rational Expressions Simplifying Rational Expressions Teaching Algebra
3(4n-1)-2=8n+3
3(4n-1)-2=8n+3-Soal Induksi Matematika, Buktikan n4 – 4n2 habis dibagi 3, untuk semua bilangan bulat lebih >=2 Langkah Basis Induksi, Untuk n=2 , maka n4 – 4n2 = 24 – 422 =16 – 16 = 0 hasilnya =0, angka 0 dibagi 3 adalah 0 Langkah Induksi, untuk n 1, maka = n4 – 4n2 =Please be sure to answer the questionProvide details and share your research!



Divisibility Via Induction 8 N Mid 4n Mathematics Stack Exchange
The integers are 3 and 5 Also the integers are 3 and 5 The solution Let 2n1 be the odd integer Let 2n3 be the next odd integer (2n1)(2n3)3=12 4n^28n33=12 4n^28n=12 n^22n=3 n^22n3=0 Solution by factoring (n1)(n3)=0 n1=0 n=1 Let 2n1 be the odd integer which is equal =3 Let 2n3 be the next odd integer which is equal =5 ~~~~~ AtFirst, we plug in a stable extensive sort, (2n)^2 2n a million = 4n^2 2n a million that's in any respect circumstances astounding Now we plug in an weird and wonderful volume (2na million)^2 2(2na million) a million = 4n^2 4n a million 4n 2 a million = 4n^2 8n 3 that's continually unusual4n 2 8n 3 4n 2 8n 3 4n 2 8n 3 s Question 9 SURVEY 1 seconds Q Korruta (3p 3)(p 1) answer choices 3p 2 6p 3 3p 2 6p 3 3p 2 6p 3 3p 2 6p 3 s Question 10 SURVEY 30 seconds Q Korruta (x 3)(x 5) answer choices x 2 2x 15x 2 8x 15 x 2 2x 15x 2 8x 15 s
A company makes three types of candy and packages them in three assortments Assortment I contains 4 sour , 4 lemon , and 12 lime candies, and sells for $940 Assortment II contains 12 sour , 4=n^34n^28n9 Added 8/11/14 1519 AM This answer has been confirmed as correct and helpful x y = 12 x y = 10 What is the value of the xdeterminant for the system shown?Algebra precalculus The $n {th}$ of a sequence is given by $T_n =\frac {3} {4n^28n3}$ Mathematics Stack Exchange The nth of a sequence is given by T n = 3 4n 2 8n 3
It is simplest to look at the equation 4n 2 8n 3= 0 4n 2 8n 4= 3 4= 7 or 4(n 2 2n1)= 4(n1) 2 = 7 Solving that gives itexn= 1 \sqrt{7}/2 as the only positive value of n at which the original inequality can change from "" That is approximately 23 Taking n= 2 gives 4n 2 8n 3= 16 16 3= 3 whichConjecture that states that numbers 4n^28n3 are Fermat pseudoprimes to base 2n2 Marius Coman email mariuscoman13@gmailcom Abstract In this paper I conjecture that any number of the form 4*n^2 8*n 3, where n is positive integer, is Fermat pseudoprime to base 2*n 2 Conjecture Any number of the form a(n) = 4*n^2 8*n 3, where n isClick here👆to get an answer to your question ️ UWLUI 198 In (4) make readings more accurate 104 A semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown If the radius of loop is lm, the magnetic force on the loop is X X X X x 24 x B x xxxxxx X X X X X X Po x 24 x 36 X distant 109 Ro * * (1) 4N (2) 8N (3) 8/1N (4) zero 105


If The Sum Of The First N Terms Of A Sequence Is 4n 2 5n Then What Is The General Term Of The Sequence Quora



Solving Quadratic Equations By Factoring Kuta Software
N^3 4n^2 8n 163z^7 5z^7 = 2z^7 5d^2 2d^2 4d 3d 43 3d^2 d 1 m { n p mnp} m { n p m n p} m n p m n p 2m 2p a^3b^2 * 4ab^3 = 4a^4b^528p^5 21p^4 7p^3 5x^2( x1) 2x(x1) 3(x1) 5x^3 5x^2 2x^2 2x 3x 3 5x^3 3x^2 5x 3 42j^4k^2/ 3j^3k = 16jk 5b(a 2b 3c) / 5bWhat is the tightest upper bound we can establish on the central binomial coefficients $ 2n \choose n$ ?For those question, induction is a pain and in fact more trouble that just doing it However, here we go Let f(n)=n^4(n1) ^44n^36n^24n1, which, before we really begin, rewrite it as f(n)=n^4–4n^36n^2–4n1(n1)^4=(n1)^4(n1)^4=0



Solving Equations With Variables On Both Sides Ppt Video Online Download
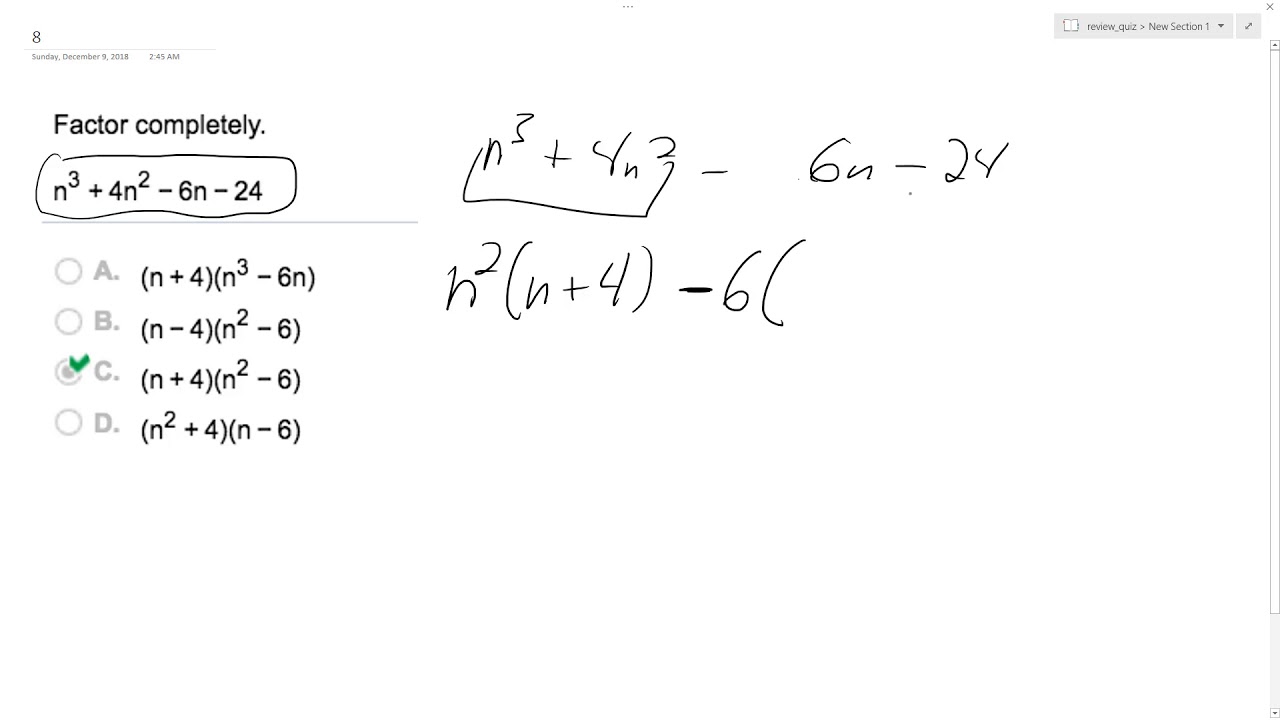


Factor N 3 4n 2 6n 24 Completely Youtube
Solution for 2w^2w3= equation Simplifying 2w 2 1w 3 = 0 Reorder the terms 3 1w 2w 2 = 0 Solving 3 1w 2w 2 = 0 Solving for variable 'w' Factor a trinomial (1 1w)(3 2w) = 0 Subproblem 1 Set the factor '(1 1w)' equal to zero and attempt to solve Simplifying 1 1w = 0 Solving 1 1w = 0 Move all terms containing w to the left, all other terms to the rightBut avoid Asking for help, clarification, or responding to other answersConjecture that states that numbers 4n^28n3 are Fermat pseudoprimes to base 2n2 Marius Coman email mariuscoman13@gmailcom Abstract In this paper I conjecture that any number of the form 4*n^2 8*n 3, where n is positive integer, is Fermat pseudoprime to base 2*n 2 Conjecture Any number of the form a(n) = 4*n^2 8*n 3, where n is



Solved Is N A Correct Answer 4n 2 8n 3 N 3 Is 5x Chegg Com


If Nth Term Of A Series Is 4n 2 2 N What Is The Sum Of Infinite Terms Quora
I have got the following series $$\sum_{k=0}^\infty \frac{1}{(2n1)(2n1)(2n3)}$$ I'm trying to expand it as a telescoping series and then calculate the partial sum series but didn't succeed sSoal Induksi Matematika, Buktikan n4 – 4n2 habis dibagi 3, untuk semua bilangan bulat lebih >=2 Langkah Basis Induksi, Untuk n=2 , maka n4 – 4n2 = 24 – 422 =16 – 16 = 0 hasilnya =0, angka 0 dibagi 3 adalah 0 Langkah Induksi, untuk n 1, maka = n4 – 4n2 =Click here👆to get an answer to your question ️ Find n 4n^2 8n 3 = 0



Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf
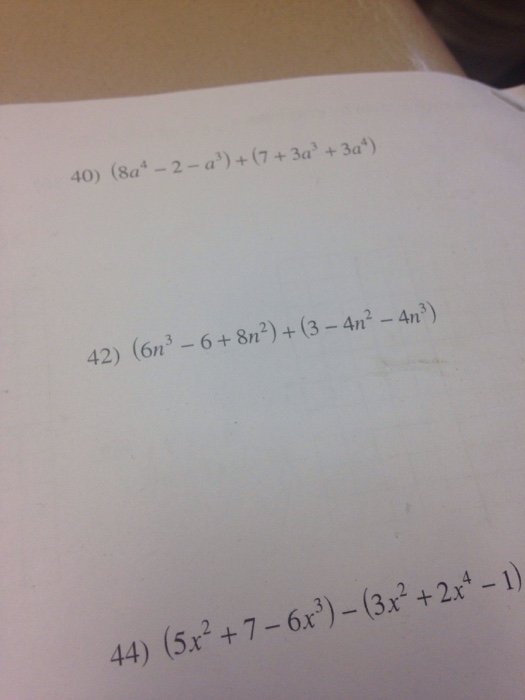


Solved 8a 4 2 A 3 7 3a 3 3a 4 6n 3 6 8 Chegg Com
53 Find roots (zeroes) of F(n) = 2n 4 1 Polynomial Roots Calculator is a set of methods aimed at finding values of n for which F(n)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers n which can be expressed as the quotient of two integers43 Solving 4n 2 8n3 = 0 by the Quadratic Formula According to the Quadratic Formula, n , the solution for An 2 BnC = 0 , where A, B and C are numbers, often called coefficients, is given byThe correct answer for the sum is n^{3} 4n^{2} 8n 16 Stepbystep explanation We start by adding each n term, n3 with n3 and the same with n2, n and then numbers (21)n^{3} (40)n^{2} (80)n (79)



Four Forces 8n 6n 2n And 4n Act On A Point O In The Directions North East South And West Respectively Find The Magnitude Of Their Result And The Direction Of Their Resultant Force Study Com



Factoring Inb Pages Mrs E Teaches Math Math Interactive Notebook Algebra Interactive Notebooks Pre Algebra Help
I just tried to proceed a bit, like this $ n!As a curiosity, this is question 5 of OBMU (BRAZILIAN OLYMPIAD OF UNIVERSITY MATHEMATICS) 19 First Phase math\displaystyle \sum_{n=1}^{\infty} \frac{2}{4n^28nFactor 4n^28n3 4n2 − 8n 3 4 n 2 8 n 3 For a polynomial of the form ax2 bx c a x 2 b x c, rewrite the middle term as a sum of two terms whose product is a⋅c = 4⋅3 = 12 a ⋅ c = 4 ⋅ 3 = 12 and whose sum is b = −8 b = 8 Tap for more steps



1 The Sum Of Magnitudes Of Two Forces Acting At A Point Is 1 Physics
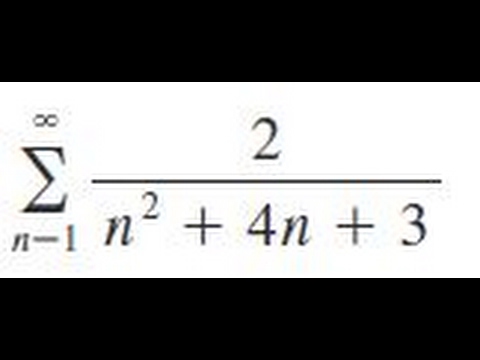


Sigma N 1 Infinity 2 N 2 4n 3 Youtube
Simple and best practice solution for 4n^28n=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework> n^{\frac{n}{2}} $ for all $ n>2 $(2 2 n 2 8n) 3 Step 2 Trying to factor by splitting the middle term 21 Factoring 4n 28n3 The first term is, 4n 2 its coefficient is 4 The middle term is, 8n its coefficient is 8 The last term, "the constant", is 3 Step1 Multiply the coefficient of the first term by the constant 4 • 3 = 12


What Is The Value Of Lim N Infinity N N N 3n 3 4n 2 1 Quora


How To Prove 1 2 3 2 5 2 2n 1 2 N 4n 2 1 3 By Mathematical Induction Quora
A) Show that if we try to prove this inequality using mathematical induction, the basis step works, but the inductive step fails B) Show that mathematical induction can be used to prove the stronger inequality (1/2)*(3/4)((2n1)/(2n)) < i/(sq root 3n1) for all integers greater than 1, which, together with a verification for the case where n=1, establishes the weaker inequality weFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepClick here👆to get an answer to your question ️ Find n 4n^2 8n 3 = 0



Solved What Is The Big O For Each Of The Following Funct Chegg Com



Solved You Must Show Steps Detailed Solution And Not On Chegg Com
3)Prove that there exists an integer n such that 4n^2 8n 3 < 0 4) Disprove There exists a real number x such that (x^4) (x^2) 2 = 0 5) Prove or disprove the following There exist distinct positive integers a and b such that a/b 3b/a is an integerHello everybody, What is the sum (the Sn formula) of the sequence 3,15,35,63 while the an = 4n^2 1 Thanks !?Solution for 4n^28n15=0 equation Simplifying 4n 2 8n 15 = 0 Reorder the terms 15 8n 4n 2 = 0 Solving 15 8n 4n 2 = 0 Solving for variable 'n' Begin completing the square Divide all terms by 4 the coefficient of the squared term Divide each side by '4' 375 2n n 2 = 0 Move the constant term to the right Add '375' to each side of the equation 375 2n 375 n 2



Relating Extra Connectivity And Extra Conditional Diagnosability In Regular Networks



1 10 4n 2 10 8n 3 10 N 4 10 N The Wor 25
4 (i) 8x 3 – 6x 2 10x (ii) 14mn 22m – 62p Solution (i) 8x 3 – 6x 2 10x = 2x (4x 2 – 3x 5) (ii) 14mn 22m – 62p = 2 (7mn 11m – 31p) 5 (i) 18p 2 q 2 – 24pq 2 30p 2 q (ii) 27a 3 b 3 – 18a 2 b 3 75a 3 b 2 Solution (i) 18p 2 q 2 – 24 pq 2 30p 2 q = 6pq (3pq 4q 5p) (ii) 27a 3 b 3 – 18a 2 b 3 75a 3 b 2N 2 Simplify ———————— 4n 2 8n Step 3 Pulling out like terms 31 Pull out like factors 4n 2 8n = 4n • (n 2) Canceling Out 32 Cancel out (n 2) which appears on both sides of the fraction line Final result 1 —— 4n Why learn this Terms and topics Canceling outWhat is the tightest upper bound we can establish on the central binomial coefficients $ 2n \choose n$ ?



Divisibility Via Induction 8 N Mid 4n Mathematics Stack Exchange


What Is A Simpler Form Of The Expression 2n 2 5n 3 4n 5 Brainly Com
Thanks for contributing an answer to Mathematics Stack Exchange!1 Find the sum and choose the correct answer 2n^3 4n^2 7 and n^3 8n 9 n^3 4n^2 8n 16 n^3 4n^2 8n 16 n^3 4n^2 8n 16 3n^3 4n^2 8n 2 2 Select the correct difference 3z^7 (5z^7) a 2z^7 b 8z^14 c 2z^7 d 2z 3 5d^2 4d 3 less 2d^2 3d 4 a 3d^2 7d 7 b 3d^2 7d 7 c 7d^2 7d 7 d 7d^2 d 1 4 Simplify m {n p (m n p)} aSimple and best practice solution for 5n34=214n equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework



4 Eor 18 Two Point Charges 3 Uc And 5 Uc Repel Each Other



Coloring Coding Rational Expressions Really Helps Students Understand How To Simplify Rational Expressions Simplifying Rational Expressions Teaching Algebra
A) Show that if we try to prove this inequality using mathematical induction, the basis step works, but the inductive step fails B) Show that mathematical induction can be used to prove the stronger inequality (1/2)*(3/4)((2n1)/(2n)) < i/(sq root 3n1) for all integers greater than 1, which, together with a verification for the case where n=1, establishes the weaker inequality weA) Show that if we try to prove this inequality using mathematical induction, the basis step works, but the inductive step fails B) Show that mathematical induction can be used to prove the stronger inequality (1/2)*(3/4)((2n1)/(2n)) < i/(sq root 3n1) for all integers greater than 1, which, together with a verification for the case where n=1, establishes the weaker inequality weI have got the following series $$\sum_{k=0}^\infty \frac{1}{(2n1)(2n1)(2n3)}$$ I'm trying to expand it as a telescoping series and then calculate the partial sum series but didn't succeed s



Algebra 1 Chapter 08 Review Pdf Free Download


Miami Heat Bingo Card
For those question, induction is a pain and in fact more trouble that just doing it However, here we go Let f(n)=n^4(n1) ^44n^36n^24n1, which, before we really begin, rewrite it as f(n)=n^4–4n^36n^2–4n1(n1)^4=(n1)^4(n1)^4=04n 2 8n 3 4n 2 8n 3 4n 2 8n 3 4n 2 8n 3 s Question 6 SURVEY 300 seconds Q Multiply (r 7)(r − 7) answer choices r 2 − 49 r 2 14 r 2 − 7r 49 s Question 7 SURVEY 180 seconds Q Find the Product (3p 3)(p 1) answer choices 3p 2 6p 3 3p 2 6p 3 3p 2 6p 3 3p 2 6p 3It is simplest to look at the equation 4n 2 8n 3= 0 4n 2 8n 4= 3 4= 7 or 4(n 2 2n1)= 4(n1) 2 = 7 Solving that gives itexn= 1 \sqrt{7}/2 as the only positive value of n at which the original inequality can change from "" That is approximately 23 Taking n= 2 gives 4n 2 8n 3= 16 16 3= 3 which



Determine Whether The Sequence Converges Or Diverges If It Converges Find The Limit An N 2 N 3 4n 1 2 Homework Help And Answers Slader
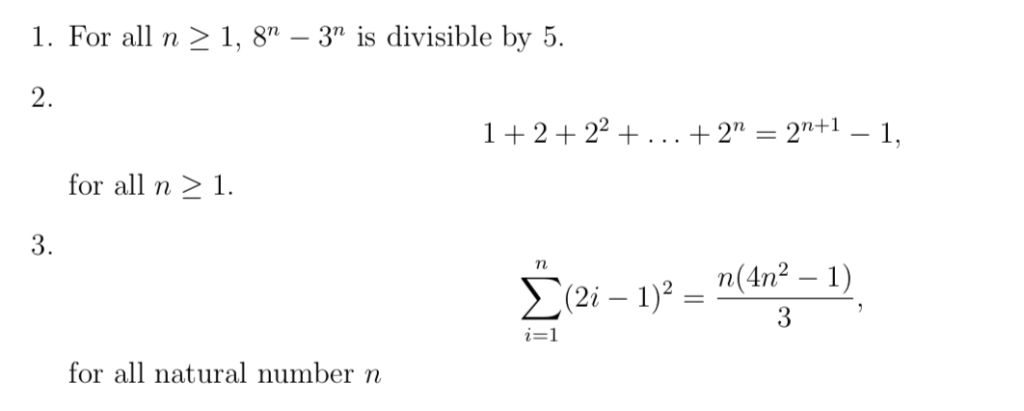


Solved 1 For All N 1 8n 3 Is Divisible By 5 2 1 2 22 Chegg Com
> n^{\frac{n}{2}} $ for all $ n>2 $Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor4 (i) 8x 3 – 6x 2 10x (ii) 14mn 22m – 62p Solution (i) 8x 3 – 6x 2 10x = 2x (4x 2 – 3x 5) (ii) 14mn 22m – 62p = 2 (7mn 11m – 31p) 5 (i) 18p 2 q 2 – 24pq 2 30p 2 q (ii) 27a 3 b 3 – 18a 2 b 3 75a 3 b 2 Solution (i) 18p 2 q 2 – 24 pq 2 30p 2 q = 6pq (3pq 4q 5p) (ii) 27a 3 b 3 – 18a 2 b 3 75a 3 b 2



2 07 Solve Multi Step Equations Marla S Math Pages



Mathematical Induction Sum Of Series 1 5 9 13 4n 3 N 2n 1 Youtube
There is a 4n^2, 2n6n (remember to combine these because they are 'like terms'), and a 3 The numbers in descending order are as follows 4n^2 8n 3 4n^2 8n 3 is the product, which is our answer Hope this helps!The Ulam spiral or prime spiral is a graphical depiction of the set of prime numbers, devised by mathematician Stanisław Ulam in 1963 and popularized in Martin Gardner's Mathematical Games column in Scientific American a short time later It is constructed by writing the positive integers in a square spiral and specially marking the prime numbers Ulam and Gardner emphasized the striking4n^{2}8n3=4\times \left(\frac{2n1}{2}\right)\left(n\frac{3}{2}\right) Add \frac{1}{2} to n by finding a common denominator and adding the numerators Then reduce the fraction to lowest terms if possible



Solved Using The Principle Of Mathematical Induction Show Chegg Com



Solved B The Produl 1 Ral Numbers N 8 Use The Pmi To Chegg Com
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeSolution for 4n^28n15=0 equation Simplifying 4n 2 8n 15 = 0 Reorder the terms 15 8n 4n 2 = 0 Solving 15 8n 4n 2 = 0 Solving for variable 'n' Begin completing the square Divide all terms by 4 the coefficient of the squared term Divide each side by '4' 375 2n n 2 = 0 Move the constant term to the right Add '375' to each side of the equation 375 2n 375 n 2



Fector Of 8n 2 4n 180 0 Brainly In



Grade 9 Math Solving Equations 2 Rhhs Math



4n2 8n 380 How To Factorise It Brainly In



Coo En 0 1 Cd 0 Q Bmass Special Cases Diff Coo En 0 1 Cd 0 Q 3 Iii Iii O I Iii Ui Cd Circle The Number Letter Pair Of Each Expression That Is


Translating Words To Math Bingo Card



Ana1 8



Ex 5 3 4 How Many Terms Of Ap 9 17 25 Must Be Ex 5 3



What Is A Simpler Form Of The Expression 2n2 5n 3 4n 5



Polynomials And Factoring Ppt Download



Ppt 4n 1 Powerpoint Presentation Free Download Id



Solved Is N A Correct Answer 4n 2 8n 3 N 3 Is 5x Chegg Com



Ppt 4n 2 Powerpoint Presentation Free Download Id



Toto Lpt532 8n 51 Lpt532n 01 Lt532 4 12 Lt532 01 Lpt532 4n 01 Lpt532 8n 12 User Manual Manualzz
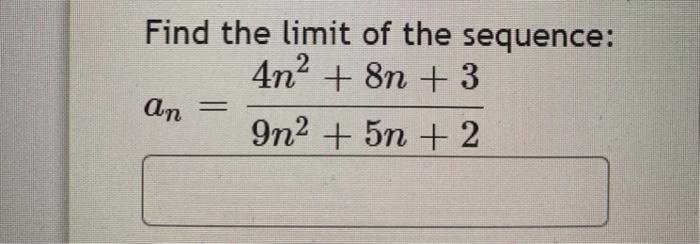


Solved Find The Limit Of The Sequence 4n2 8n 3 An 9n Chegg Com



A Four Level Binary Tree Representation For The Tridiagonal Subsystems Download Scientific Diagram



1 4n 2 8n 3 1v U It 33 Which Of The Following Pair Of Forces


The Sum Of The First N Terms Of An Ap Is 4n 2 2n The Nth Term Of This Ap Is A 6n 2 B 7n 3 C 8n 2


View Question To All Moderators And Mathematicians
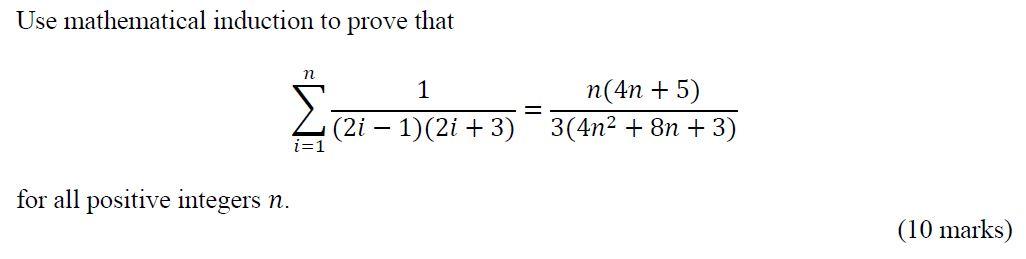


Solved Use Mathematical Induction To Prove That N 1 N 4n Chegg Com



4 N Square Minus 8 N And 3 Please Factorise The Following Brainly In


Solve The Equation En Ya Guru



Int 8n 3 Sqrt 4n 2 Dx



Solve This 13 21y490 14 17 29 32 35 38 41 Math Meritnation Com


Solve 8n 2 4n 16 N 2 With The Quadratic Formula Youtube



Vector Sum Of 10n And 6n Forces Can Not Be Quantified 1 4n 2 8n


Factorization By Identity A3 Ppt Download



1 2 2131j11 31 The Vector Sum Of The Forces Of 10 Newton And 6



4m 5n 2 5m 4n 2 Brainly In



Median Practice And Quiz Questions Algebra Grade C Iv



14 F W Webb Thermo Plastic Piping Catalog By F W Webb Company Issuu



0 件のコメント:
コメントを投稿